[Unity] Vector에 대하여

---

VECTOR

Unity에서 오브젝트의 속도와 위치를 저장할 때 x, y, z 세 원소를 가지는 3D벡터인 vector3 타입을 사용했습니다.

오브젝트의 위치, 방향, 회전, 속도, 크기는 모두 vector 형식으로 저장됩니다. 따라서 vector는 Unity에서 매우 중요합니다.

이번시간에는 vector에 대해서 알아보겠습니다.

---

#Vector의 정의

Vector는 공간상의 화살표, 나열된 숫자 데이터 등 다양한 관점이 있습니다. 하지만 Unity에서의 Vector는 공간상의 화살표로 사용됩니다. Unity에서의 Vector는 위치, 방향, 속도를 나타냅니다.

벡터는  x, y, z에 대응 하는 세 원소를 가지고 있고 오브젝트의 위치, 방향, 회전, 속도, 크기는 모두 vector 형식으로 저장됩니다. 

---

#절대 위치와 상대 위치

 

상대 좌표 : 현재 좌표의 기준

절대 좌표 : Unity 가상 공간의 기준인 좌표

 

만약 (1, 1) 만큼 이동한다고 하면 상대 좌표는 현 위치에서 상대적으로 어느 방향으로 얼만큼의 크기로 갈것인지 표현합니다.

하지만 절대 좌표는 Unity의 가상 공간의 원점이 (0, 0)이라고 가정하면 (0, 0)에서 x 방향으로 1 칸, y 방향으로 1칸 이동하는 좌표로서 의미를 갖는다.

---

#Vector의 크기

2D 벡터 (-3, 4)를 예시로 해봅시다. 

(-3, 4) 의 방향은 (-3, 4)로 향하는 화살표의 방향입니다. 

화살표를 빗볏으로 하는 직각삼각형의 빗변이 (-3, 4)의 vector의 크기 입니다.

피타고라스 정리를 이용하여 빗변을 구할 수 있습니다.

 

$$h=\sqrt{a^2+b^2}$$

 

따라서 (-3, 4)의 크기는 5 입니다.

• Vector의 크기는 화살표의 길이에 대응하기 때문에 음수 X
• Vector의 방향과 크기는 별개의 값

---

#Vector의 스칼라 곱

벡터에서 배수를 취하는 숫자를 곱하는것을 스칼라 곱이라고 합니다. 여기서 곱하는 수를 스칼라 라고 부릅니다.

 

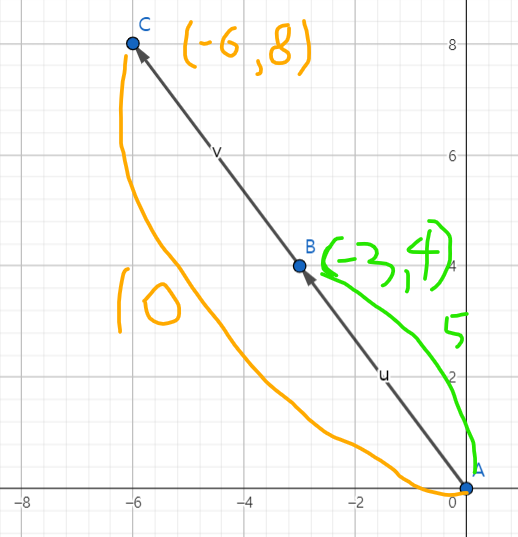
(-3, 4) 크기는 5, (-6, 8)의 크기는 (-3, 4)의 2배인 10 입니다. 

(-3, 4)에다가 2를 곱해보면 

2 x (-3, 4) = (-3 x 2, 4 x 2) = (-6, 8) 의 크기는 (-3, 4)의 크기의 2배인 10이다.

벡터에서 스칼라 곱을 곱하면 벡터의 각 원소에 개별적으로 곱셈이 적용됩니다.

따라서 스칼라  값은 기존 벡터를 방향은 그대로 유지하면서 길이는 늘리거나 줄이는 배율 입니다.

---

#Vector덧셈과 뺄셈

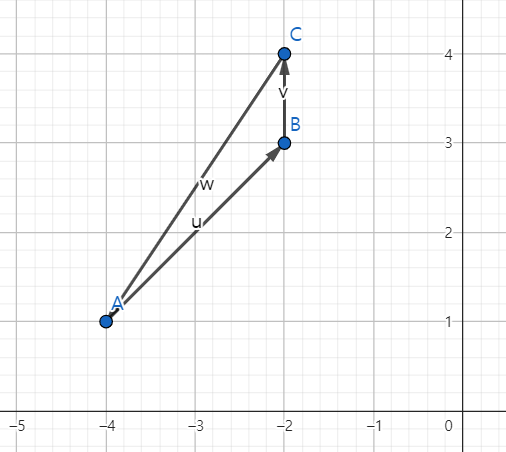
A(-4, 1)인 점에서 B(-2, 3)을 더하면 (-4, 1) + (-2, 3) = (-4, + -2, 1 + 3) = (-2, 4)

두 벡터 A와 B를 더하는 행위를 공간상에서 보면 A에서 B만큼 더 이동한다는 의미 입니다.

반대로 A와 B를 빼서 좌표의 거리를 알 수 있다.

---

 

#방향 Vector

• 크기가 1인 벡터(1,1)로 정규화된 벡터(Nornalized Vector)라고 부르기도 합니다.
• 벡터의 방향을 비교할 수 있음

 

만약 (3, -3)벡터가 있다면 그 벡터의 시작지점에서 반지름인 1인 원을 그랴서 바깥부분을 잘라내고 난뒤에값 (0.71, -0.71)가 됩니다.

하지만 방향벡터는 크기가 1 이어야 됩니다.

그래서 정규화를 시키면 크기가 1이 됩니다.  -> 결과 : (1, -1)

---

#Vector의 내적

내적은 두 벡터의 곱셈 연산으로 구해지는 스칼라 값을 의미합니다. 내적을 계산할 때는 두 벡터의 크기와 각도가 중요합니다. 두 벡터 a와 b의 내적은 다음과 같이 계산됩니다.

a · b = |a||b|cosθ

여기서 |a|는 벡터 a의 크기, |b|는 벡터 b의 크기, θ는 벡터 a와 b가 이루는 각을 나타냅니다. 두 벡터가 수직이면 내적은 0이 됩니다. 또한, 두 벡터가 같은 방향을 가지면 내적은 두 벡터의 크기를 곱한 값과 같습니다. 반면, 두 벡터가 반대 방향을 가지면 내적은 두 벡터의 크기를 곱한 값에 -1을 곱한 값과 같습니다.

내적은 두 벡터 사이의 각도와 크기를 고려하여 벡터의 길이를 찾는 등 다양한 계산에 사용됩니다. 예를 들어, 두 벡터가 이루는 각도를 구하고 싶다면 내적을 사용하여 계산할 수 있습니다.

---

#Vector의 외적

외적은 두 벡터의 곱셈 연산으로 구해지는 벡터 값을 의미합니다. 외적을 계산할 때는 두 벡터의 크기와 각도가 중요합니다. 두 벡터 a와 b의 외적은 다음과 같이 계산됩니다.

a x b = |a||b|sinθn

여기서 |a|는 벡터 a의 크기, |b|는 벡터 b의 크기, θ는 벡터 a와 b가 이루는 각을 나타냅니다. n은 두 벡터에 수직인 벡터를 의미합니다. 따라서 n은 a와 b가 이루는 평면의 법선 벡터입니다.

외적은 두 벡터 사이의 각도와 크기를 고려하여 벡터의 방향과 크기를 찾는 등 다양한 계산에 사용됩니다.

---

#유니티 C# Vector

이제 Unity에서의 Vector를 알아보자

---

#Vector 타입

Vector 3 a = new Vector(0, 0, 0,) //(x, y, z) 벡터 생성
a.x = 20; //(20, 0, 0)
a.y = 10; //(20, 10, 0)
a.z = 1; //(20, 10, 1)

 

 

• 유니티에는 Vector2, Vector3, Vector4 를 지원함
• Vector구조체로 선언되어 있으며 Vector3에는 x, y, z가 float형으로 있다.

---

#Vector 연산

---

#스칼라 곱

Vector3 vec = new Vector3(1, 2, 3)
a = a * 10; //a(10, 20, 30);

---

#Vector의 덧셈과 뺄셈

 

Vector3 + Vector3; //덧셈

Vector3 - Vector3; //뺄셈

---

#Vector의 정규화

Vector3.normalized;

 

---

#Vector의 크기

Vector3.magnitude;

---

#Vector의 내적, 외적

Vector3.Dot(a, b); //내적
Vector3.Cross(a, b); //외적

---

#Gimbal Lock

Unity에서 짐벌락은 3D 공간에서 오브젝트의 방향을 나타내는 Euler 각도를 사용할 때 발생하는 문제입니다. 이 문제는 선형대수학에서 사용되는 회전 행렬의 불안전성과 관련이 있습니다.

짐벌락은 세 개의 회전 축(x, y, z)을 사용하여 오브젝트의 방향을 나타내는 Euler 각도에서 발생합니다. 이 경우, 오브젝트가 특정 방향에서 다른 방향으로 회전할 때, 두 축이 일치하는 순간이 발생합니다. 이때, 회전 축이 서로 겹치게 되면 짐벌락이 발생하게 됩니다.

 

이러한 짐벌락은 오브젝트의 방향을 제대로 나타내지 못하게 되며, 예기치 않은 움직임으로 이어질 수 있습니다. 따라서 Unity에서는 Quaternion을 사용하여 회전을 처리합니다. 이를 통해 짐벌락 문제를 회피할 수 있습니다.

 

Quaternion은 Euler 각도 대신 회전각과 회전축을 사용하여 회전을 처리합니다. 이를 통해 짐벌락 문제를 회피할 수 있으며, 안정적인 회전을 처리할 수 있습니다.

Unity에서 짐벌락 문제를 해결하기 위해서는 Quaternion을 사용해야 하며, Euler 각도를 사용하지 않도록 주의해야 합니다. 또한, Quaternion을 사용하여 회전을 처리할 때, Quaternion과 Euler 각도 간의 변환 함수를 사용하여 변환이 필요한 경우에도 안정적인 회전을 처리할 수 있습니다.

---

#Quternion

쿼터니언은 4차원 벡터(x, y, z, w)로 표현되어서 사원수라고도 부릅니다. 이 벡터는 3차원 공간에서의 회전 축(axis)과 회전각(rotation angle)으로 구성됩니다. 즉, 쿼터니언은 3차원 공간에서의 회전을 4차원 공간으로 확장시킨 것입니다.

 

Unity에서는 쿼터니언을 사용하여 오브젝트를 회전시킵니다. Unity의 Transform 컴포넌트에는 rotation 속성이 있습니다. 이 속성은 쿼터니언 값을 가집니다. 오브젝트를 회전시키기 위해 rotation 속성을 변경하면 됩니다.

 

쿼터니언은 회전에 대한 여러 가지 이점을 제공합니다. 예를 들어, 쿼터니언은 회전의 순서를 고려하지 않으므로 회전이 뒤섞이는 문제를 해결할 수 있습니다. 또한, 쿼터니언은 오일러 각도(Euler angles)보다 계산이 더 빠르고 정확하며, gimbal lock 문제를 방지할 수 있습니다.

---

https://product.kyobobook.co.kr/detail/S000001810471

레트로의 유니티 게임 프로그래밍 에센스 | 이제민 - 교보문고

이 책을 보면서 공부한 내용들을 정리하였습니다.